Sum Of 1n2 From 1 To N
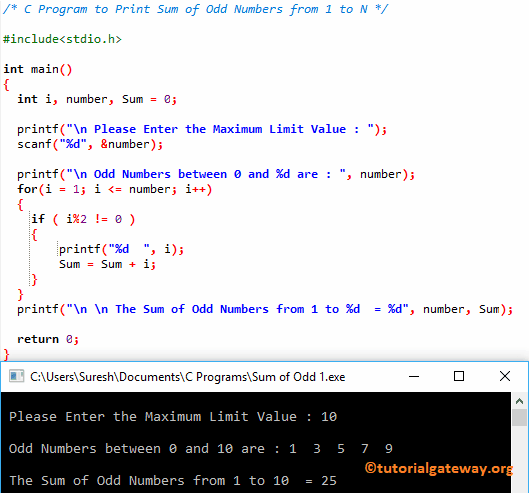
C Program To Print Sum Of Odd Numbers From 1 To N

Using Mclaurin Series To Find The Sum Of Reciprocal Squares A Minimum Of Blind Calculation

Gauss Method In The 1700s A Primary School Teacher By Can Balkaya Betamat En Medium
Www Jstor Org Stable

Mathematics Notes

Induction Mathematics For Computer Science Lecture Slides Docsity
To find the limiting sum of the series, we need to first find the partial sum of.
Sum of 1n2 from 1 to n. This way, it must by induction work for all subsequent values of n. When n is 2, it's 0 squared plus 1 squared plus 2 squared. Sum1 to n i^2 = n(n+1)(2n+1)/6 (These are well known formulas.
Free Limit of Sum Calculator - find limits of sums step-by-step This website uses cookies to ensure you get the best experience. But this doesn't really change anything, just begin applying the inequality 1/n^2 < 1/n-1 - 1/n after the 2nd term, instead of after the first. So it is like (N-1)/2 * N.
For all n, n!. Compute n = 1 ∑ ∞ n 2 + 1 1. K=1 k2 = 2 k=1 k 2 + k=1 k 1 = 2 n + 1 3 + n + 1 2 :.
The result is always n. Try to make pairs of numbers from the set. An advanced problem one of my friends gave me which I think would be interesting to discuss:.
Compute answers using Wolfram's breakthrough technology & knowledgebase, relied on by millions of students & professionals. At each iteration, add on 1/N^P from the previous iteration, then store the result in X, the current sum. But both these products diverge:.
This thread is archived. In this video (another Peyam Classic), I present an unbelievable theorem with an unbelievable consequence. N = 0.
To N/2) with (N/2+1. After having done some math for a while, one eventually comes across the beautiful result:. To show that the series given by p=1 does not converge, notice that the first n terms, grouped accordingly, give.
09/14/02 at 10:33:49 From:. To find the sum of a series of arithmetic terms (that is, terms that increase or decrease by a constant amount each term), use the formula S˯n = n(a˯1 + a˯n)/2, where n is the number of terms, a˯1 is the first term in the sequence, and a˯n is the last term in the sequence. The sequence a(n) = 1/n^2 decreases sufficiently fast, whereas b(n) = 1/n does not.
If p > 1 then the sum of the p-series is ζ(p), i.e., the Riemann zeta function evaluated at p. 11.10 - Find the sum of the series. The sequence defined by a_{n}=1/(n^2+1) converges to zero.
Assuming that m>n, we have. For the variable N (the current term in the series sum_(N=1)^(M) 1/(N^P)), we go through iterations from the 1st iteration to the Mth iteration, where M is the number of terms. When p = 1, the p-series is the harmonic series, which diverges.
\sum_{i=1}^{n} \arctan(\frac{1}{2n^2}) I have to find sum of first n terms. Don’t stop learning now. Prove that the series whose terms are 1/n^2 converges by showing that the partial sums form a Cauchy sequence.
So that's 1 plus 4, which is 5. So that's just 0. Get hold of all the important DSA concepts with the DSA Self Paced Course at a student-friendly price and become industry ready.
Explain a formula Dear Dr. The first + the last;. When n is 1, it's 0 squared plus 1 squared.
I am having trouble making a recursive method that calculates the sum of 1,2,3 to N, but does it by adding (1,2,3. Find the absolute maximum and absolute minimum values of f on the given interval. The "pieces" approach zero, but the total of "all" the pieces is positive.
In fact the condition is p>1. Sum of n + (n-1) + (n-2). The code i manage so far is this:.
Sum1 to n i = n(n+1)/2. Without using function */ #include int main() { int num,i,j,fact,sum=0;. The p-test provides a means to check quickly whether or not any series of the form.
We'd just stop right over there. Get 1:1 help now from expert Calculus tutors Solve it with our calculus problem solver and calculator. This becomes the current sum.
Show that the series 2/(n^2-1) from n=2 to infinity is convergent, and find its sum. The partial products of the first one tend to zero, and the partial products for the second one tend to infinity. Math1*1!+2*2!+3*3!++n*n/math math!/math This can be re-written as:.
Hey guys Is there function or a way that could do this in excel?. The Basel problem asks for the exact sum of this series (in closed form), as well as a proof that this sum is correct. Compute the sum of the series.
New comments cannot be posted and votes cannot be cast. The series is checked if it is converging or not by the help of the series comparison test. So when n is 0-- well, that's just going to be 0 squared.
The second + the one before last. 11.10 - Find the sum of the series. When n is 3, now we go all the.
/* This program find sum of series 1!+2!+3!+4!++n!. Namely, I use Parseval’s theorem (from Fourier ana. Solve {eq}\sum ^\infty _{n = 1} \frac{1}{n^2 \ ln \ n - 10} {/eq} Mathematical Series:.
To do this, we will fit two copies of a triangle of dots together, one red and an upside-down copy in green. For example, when z = 1, we have YN n=1 1+ 1 πn > 1+ XN n=1 1 πn, and the right hand side is a partial sum of a divergent series. The corresponding infinite series sum_{n=1}^{infty}1/(n^2+1) converges to (pi coth(pi)-1)/2 approx 1.077.
11.10 - Find the sum of the series. = sum1 to n (n+1)i - sum1 to n i^2 = (n+1) sum1 to n i - sum1 to n i^2. Get an answer for '`sum_(n=1)^oo arctan(n)/(n^2+1)` Confirm that the Integral Test can be applied to the series.
His arguments were based on manipulations that were not justified at the time, although he. \\sum _{n=1}^{\\infty } \\frac{1}{n^4} I can do 1/n^2 easily by using x^2 as a function but for this I try x^4=\\frac{1}{2\\pi }\\int_{-\\pi }^{\\pi } x^4 \\, dx+. 2.Here is a systematic method of writing a polynomial P(x) as a 0 x 0 + a 1 x 1.
Practice with binomial coe cients 1.Use this technique to nd a formula for P n k=1 k 3. {eq}\sum_{n=2}^{+\infty}\frac{2^{2n-1}}{7^{n}+3} {/eq} Sum of a Series:. Σ ln(1- 1/n 2) (Find the sum of the series from n=2 to infinity) Expert Answer 100% ( ratings) Previous question Next question Get more help from Chegg.
(3, 2) and (5, 18) b. \text {Compute } \displaystyle\sum_{n=1}^{\infty} \dfrac {1}{n^2+1}. It means n-1 + 1;.
Use the comparison test with 1/n^2. Then use the Integral Test to determine the convergence or divergence of the series. 2 n+1 3 + n+1 2 = 1 6 (2n 3 + 3n2 + n).
If observed closely, we can see that, if we take n common, series turns into an Harmonic Progression. \begin{equation} \label{ptwoseries} \sum_{n=1}^\infty \frac{1}{n^2} = \frac{1}{1^2}+ \frac{1}{2^2} + \frac{1}{3^2} + \frac{1}{4^2} + \cdots \end{equation} The Integral Test compares an infinite series to an improper integral in order to determine convergence or divergence. Asked • 10/28/16 I need help on this problem.
≥ n so then. The sum of 1/n^2 converges to a certain positive number, but the individual terms 1/n^2 approach 0. 11.10 - Find the sum of the series.
Supercharge your algebraic intuition and problem solving skills!. N=1 1− z πn and Y∞ n=1 1+ z πn. Program for finding the sum of the nth term of the series (n^2-1^2) + 2(n^2-2^2) + 3(n^2-3^2) + ….n(n^2-n^2) Examples:.
I've tried to start this as follows:. Give me please any hint. Get 1:1 help now from expert Calculus tutors Solve it with our calculus problem solver and calculator.
For the proof, we will count the number of dots in T(n) but, instead of summing the numbers 1, 2, 3, etc up to n we will find the total using only one multiplication and one division!. And since you are adding two numbers together, there are only (n-1)/2 pairs that can be made from (n-1) numbers. Either the integral test or the Cauchy condensation test shows that the p-series converges for all p > 1 (in which case it is called the over-harmonic series) and diverges for all p ≤ 1.
For math, science, nutrition, history, geography, engineering, mathematics, linguistics, sports, finance, music… Wolfram|Alpha brings expert-level knowledge and. 2 Output :3 Input :5 Output :150. When is it used?.
It should be the sum from i equals 0 to n of i squared. For example, to determine the convergence or divergence of \eqref. 11.10 - Find the sum of the series.
F(t) = t + cot (t/2), /4, 7/. You give it a number and it calculates this, till it reaches 0:. Formally said, we need to prove that if for some positive integer n we can show.
So for the first few small values of n, we have proven by demonstration that f(n) = n / (n+1). 5(?1)n?2n + 1 32n + 1(2n + 1)!. Hence for all n, 1/n^2 ≥ 1/(n!)^2 and sum(1/n^2) is known convergent series (most texts call them p-series).
Compute ∑ n = 1 ∞ 1 n 2 + 1. There are many proofs for this. Early Transcendentals, Volume I Find the slope of the line passing through each pair of points.
Our task is to prove that if it works for any positive integer value of n, then it works for n + 1. Bkn m+1−k integer n ≥ 1 Thus nX−1 k=0 km = nm+1 m +1 + lower order terms Formulas relating factorial powers and ordinary powers Stirling numbers of xn = X k (n k) xk integer n ≥ 0 the second kind Stirling numbers of xn = X k " n k # xk integer n ≥ 0. By using this website, you agree to our Cookie Policy.
The sum of the series is approximately equal to 1. 2.Now we can evaluate the sum:. The ratio test isn't really necessary at all.
Sum (1/n^2) = pi^2 / 6. Answer to Find the sum of the series. Multiply everything by pi, and then the sum is a bunch of circles with radius 1/n, and for n is all integers you get a cone like shape, whose area is proportional to pi*h/x, for h is the largest value of n, and x is something dependant on n….
Finding n(n-1)/2 in the Real World Date:. You can probably find the proofs of these online) So our. Euler found the exact sum to be π 2 / 6 and announced this discovery in 1735.
Math&Stats Undergrad Original Poster 1 point · 11 months ago. Ah, just noticed you want to show it's strictly less than 2 (when taking limits above, you will get that Sum(n = 1 to infinity)1/n^2 <= 2). So that is 1.
Math, How can n(n-1)/2 be explained in common everyday language?. (2, 1) and (4, 2) c. Now we use the formulas for the sum of n consecutive integers and the sum of the squares of n consecutive integers:.
I have no idea what to do with these arctan.
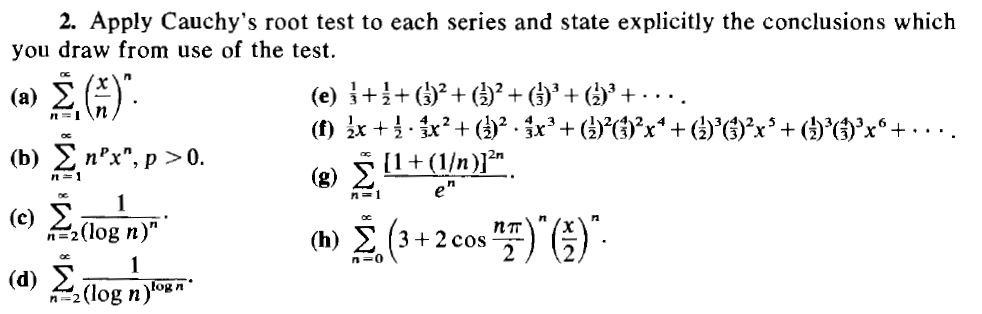
Solved Apply Cauchy S Root Test To Series Sum Of 1 Log Chegg Com

Find The Radius Of Convergence Of Sum Of 1 N X N 12 N Ln N From N 2 To Infinity Study Com

Math Origins

Example 19 Find Sum Of Series 5 11 19 29 41
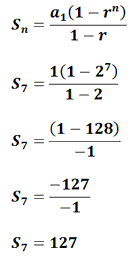
Geometric Sequences And Series

Pdf Solve Gmat Maths Tough Problems hana Wilson Academia Edu
2

Shows That The Component S 1 Of The Action The One Given By The Sum In Download Scientific Diagram

Natural Numbers Series 3 9 Sideway Output To
Q Tbn 3aand9gctfezlemn15ufmzmvbxoosov Oz Td Gz5uj0cfsjxavyylod Usqp Cau

Sum Of First N Numbers
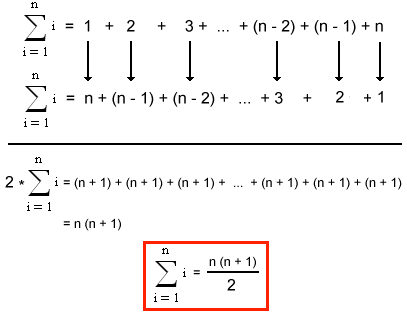
Gauss Sums The Integers

Minimum Sum Of A Pair At Least K Distance Apart From An Array

How To Sum The Integers From 1 To N 8 Steps With Pictures

Sum Of N N Or N Brilliant Math Science Wiki

How Would You Prove This Askmath

Infinite Series

Solved In N2 1 Diverge Or Converge Conditionally Or C Chegg Com

Solved The Sum Of The Series Sigma N 1 Infinity 1 N 2 Chegg Com

Find The Sum Of The Series N 1 1 N 5 Correct To Three Decimal Places Homework Help And Answers Slader
How To Find The Sum Of The Series Math Sum N 1 Infty Frac 2n 3 N N 1 N 2 Math Quora
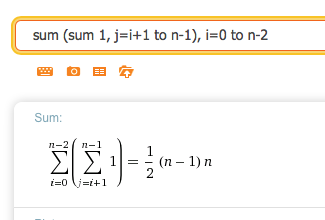
Summation Of A Summation Online Technical Discussion Groups Wolfram Community
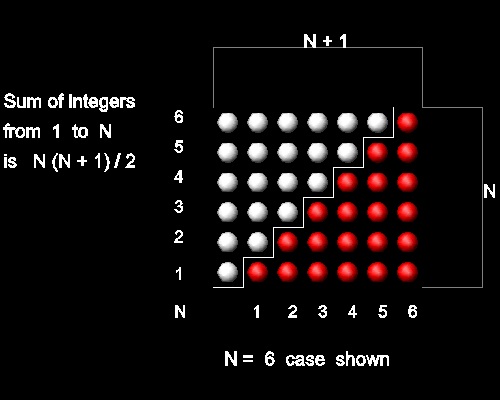
Sum Of Natural Numbers
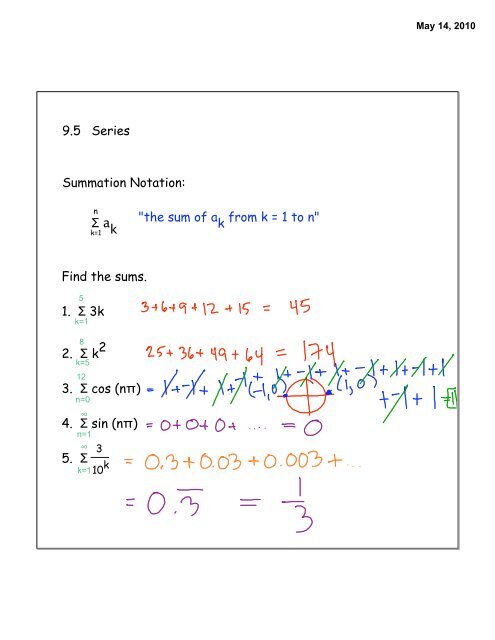
9 5 Series Summation Notation I Ak The Sum Of Ak From K 1 To N

Sum A N 2 A N 2 With N 1 And N 4 For N 1 10 1000 Download Scientific Diagram

Ex 9 4 2 Find Sum 1 X 2 X 3 2 X 3 X 4 3 X 4 X 5

A Limit Involving Binomial Coefficients Lim N To Infty 1 N Sum K 1 N 1 K N Choose K 1 K Frac12 Mathoverflow

Use Mathematical Induction To Prove That The Statements Are True For Every Positive Integer N 1 3 2 4 3 5 A N N 2 N N 1 2n 7 6 Schooltrainer Com

Practical Math 138 Assignment 10 Math 138 Uwaterloo Studocu

Basel Problem Wikipedia

Sequence And Series 02
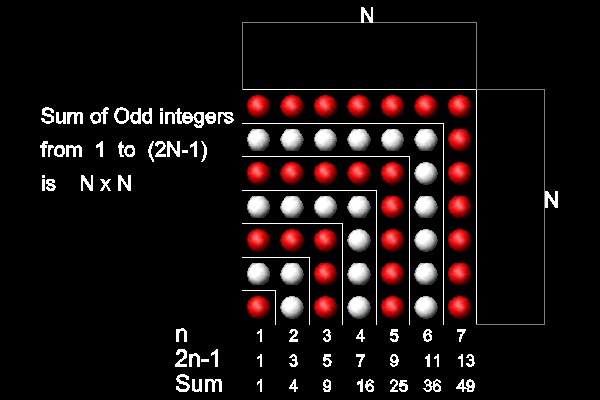
Sum Of Natural Numbers

Pdf Euler S Sum Of Powers Conjecture Thomas Mcclure Academia Edu
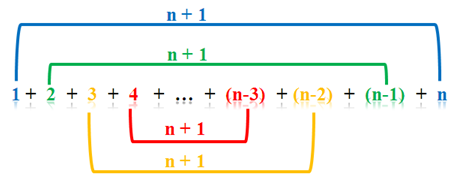
Young Gauss And The Sum Of The First N Positive Integers
Q Tbn 3aand9gctfezlemn15ufmzmvbxoosov Oz Td Gz5uj0cfsjxavyylod Usqp Cau

Summation Proof Of Sum A 3 Sum A 2 From 1 To N Mathematics Stack Exchange Mathematics Geometry Mathematics Art Fun Math
Prove That The Sum From 1 To Of 2n 1 N2 N 1 2 1 Stumbling Robot

S2 1 N 1 I Xi Xbar 2
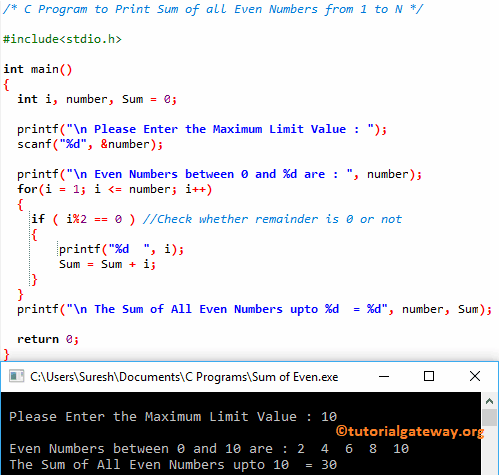
C Program To Print Sum Of All Even Numbers From 1 To N

If In An A P The Sum Of M Terms Is Equal To N And The Sum Of N Terms Is Equal To M Then Prove That Brainly In
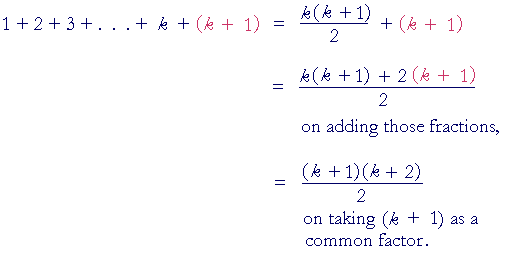
Mathematical Induction Topics In Precalculus
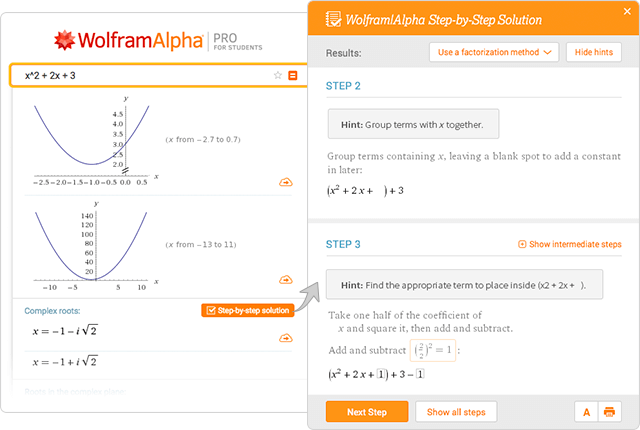
Wolfram Alpha Examples Step By Step Solutions
Prove That The Sum From 1 To Of 1 N2 1 3 4 Stumbling Robot

9 3 The Definite Integral
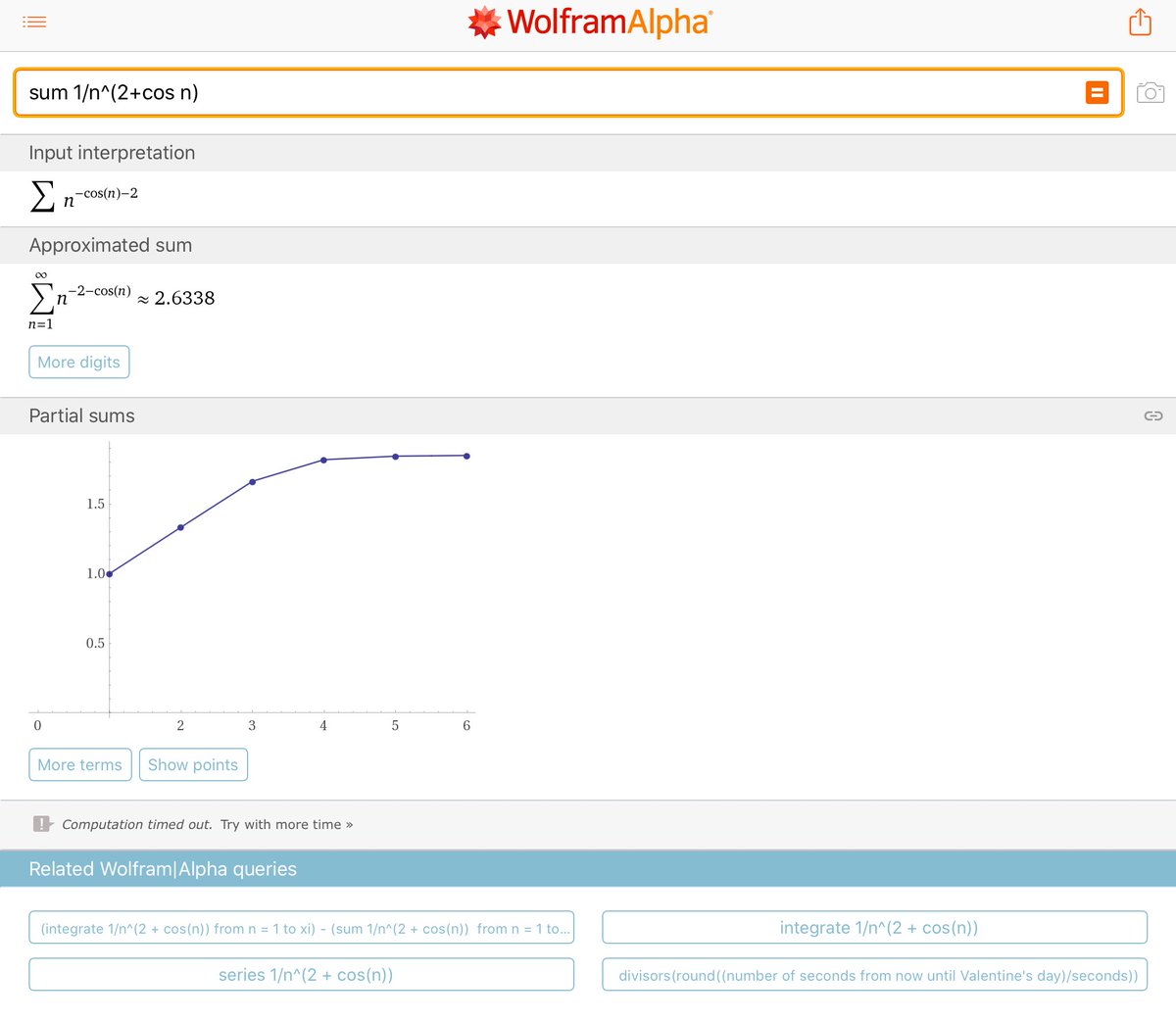
Jordan Ellenberg Now What About The Sum Of 1 N 2 Cos N
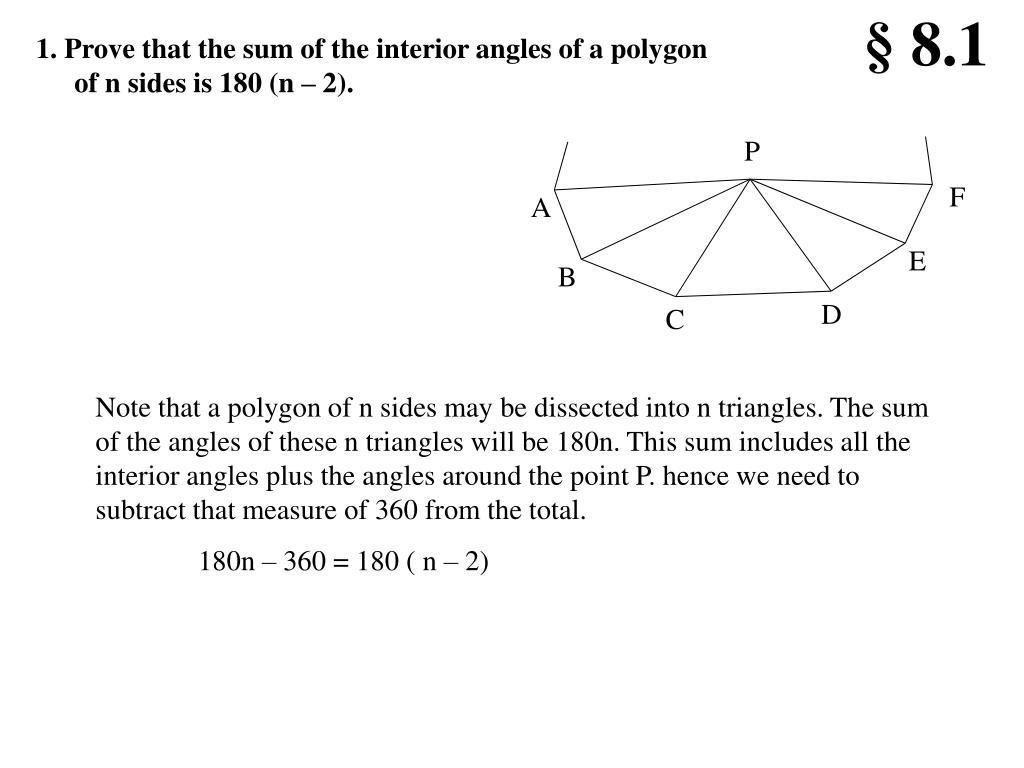
Ppt 1 Prove That The Sum Of The Interior Angles Of A Polygon Of N Sides Is 180 N 2 Powerpoint Presentation Id

Calculate The Code Complexity Of Below Code Stack Overflow

Python Program To Calculate Sum Of Even Numbers
How Do You Find The Sum Of The Infinite Geometric Series Sigma 2 2 3 N From N 0 To Oo Socratic
Http Math Uga Edu Pete Finitecalc Pdf

Psa Each Level Of Mining Productivity Costs An Approximately Equal Amount Of Ore On The Ground Also Twice The Ore Lasts Four Times As Long During That Research Factorio
Http Courses Washington Edu Tcss343 Solutions Dynamicpractice2sol Pdf
Q Tbn 3aand9gcq Tmftumer17bygo3e9h 7 Qscqrnw5niqrv Fr0rrgyg8v573 Usqp Cau

Infinite Series
How To Evaluate The Sum Of N 2 2 N From N 1 To Infinity Quora
Prove That The Sum From 1 To Of N N 1 N 2 N 3 1 4 Stumbling Robot
What Is The Sum Of X X 1 From X 1 To N Quora

The Sum Of The First N Terms Of An Arithmetic Sequence Video Lesson Transcript Study Com

Series Sigma Notation 1 Fp1 Edexcel A Level Youtube

Summation Notation Video Khan Academy
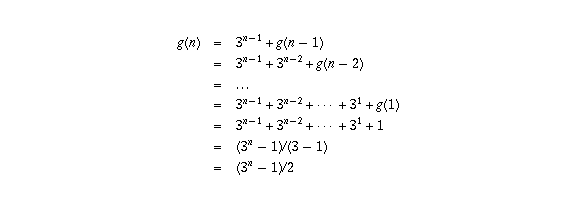
Question Corner Generalizing The Towers Of Hanoi Problem

Cube Algebra Wikipedia

If The Sum Of M Terms Of An A P Is N And Sum Of N Terms Is M Then Show That The Sum Of Its First Brainly In

Answered Subtract The Infinite Series Of Ln 1 Bartleby
How To Form The Sum Of The First N Terms Of Every Arithmetic Series Mathlibra A Math Library

Ex 9 4 9 Find Sum Of Series Nth Term Is N2 2n Class 11
2

Geometric Sequences And Sums

Data Abstraction And Problem Solving With C Walls And Mirrors 7th Edition By Carrano Henry Solutio By Jaqis2 Issuu
How Can Math Sum I 0 N N Choose I 2 N Math Be Proved Quora

Gaussian Proof For The Sum Of Squares Mathematics Stack Exchange

Sums Of Integer Powers The Faulhaber Expansion
Http Webdev Physics Harvard Edu Academics Undergrad Probweek Sol38 Pdf

Geometric Progression Series And Sums An Introduction To Solving Common Geometric Series Problems

The Sum Of All The Products Of The First N Natural Numbers Take
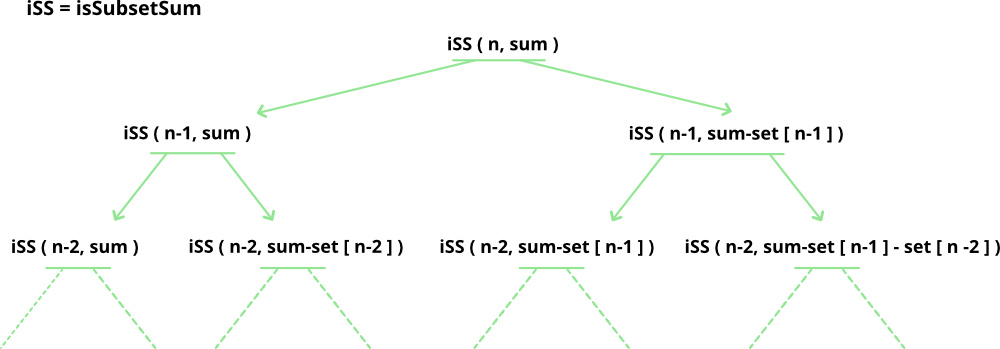
Dynamic Programming Subset Sum Problem

Sum From N 1 To N Of Sin Nx 2 N Mathematics Stack Exchange
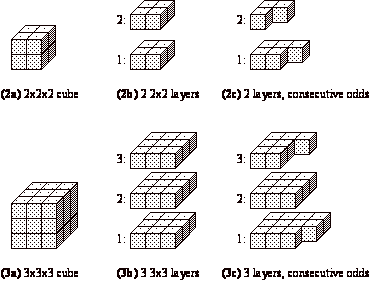
Cubes As Sums Of Odds Extended

Chapter Sequences And Series Ppt Video Online Download
Prove That The Sum From 1 To Of 2 3n 1 3 Stumbling Robot

Untitled Document
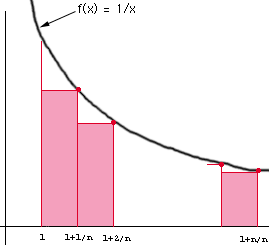
Riemann Sums

Sigma Notation The Greek Letter S Is Used To Denote Summing If The Terms Of A Sequence Are Then For Example From The 1 St Term To The 5 Th If You
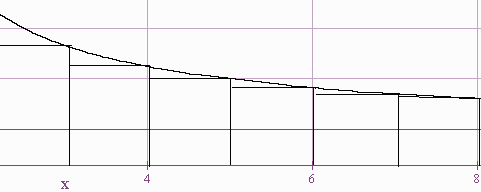
Integral Test And P Series

Maximum Sum In Circular Array Such That No Two Elements Are Adjacent Geeksforgeeks

Factorial Program In C Programming Simplified

Solved A Using Formula 2 Find The Sum Of The Series Si Chegg Com

Section 11 4 Series The Nature Of Mathematics 13th Edition
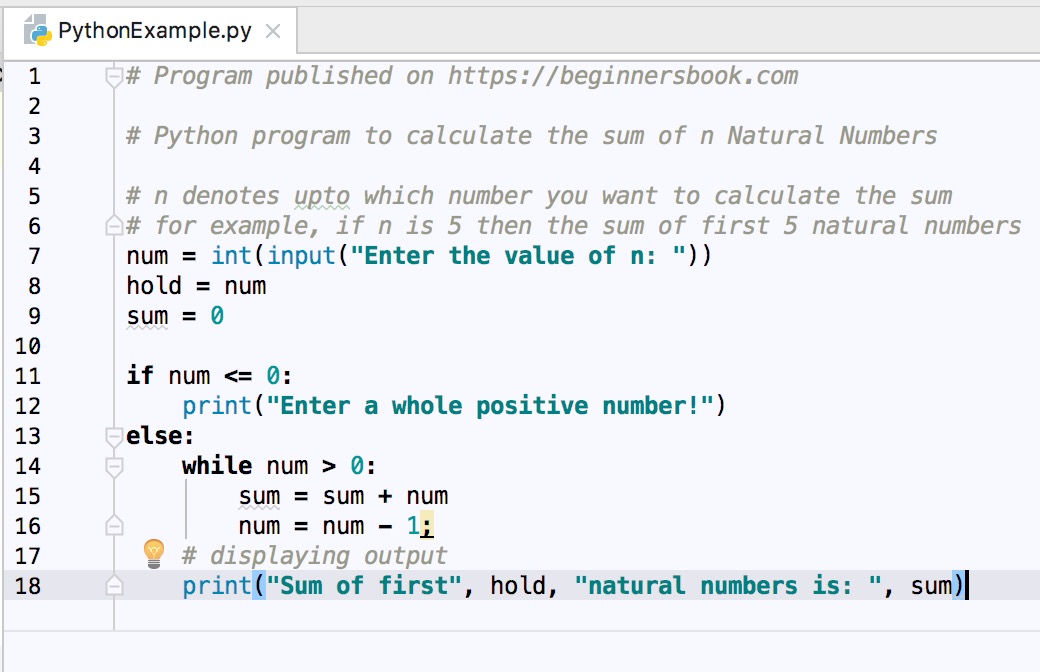
Python Program To Find Sum Of N Natural Numbers

Lack Of Understanding Of The Proof Of Sum Limits I In Mathbb Z 2 I 3 Mathematics Stack Exchange

1 2 1 4 1 8 1 16 Wikipedia
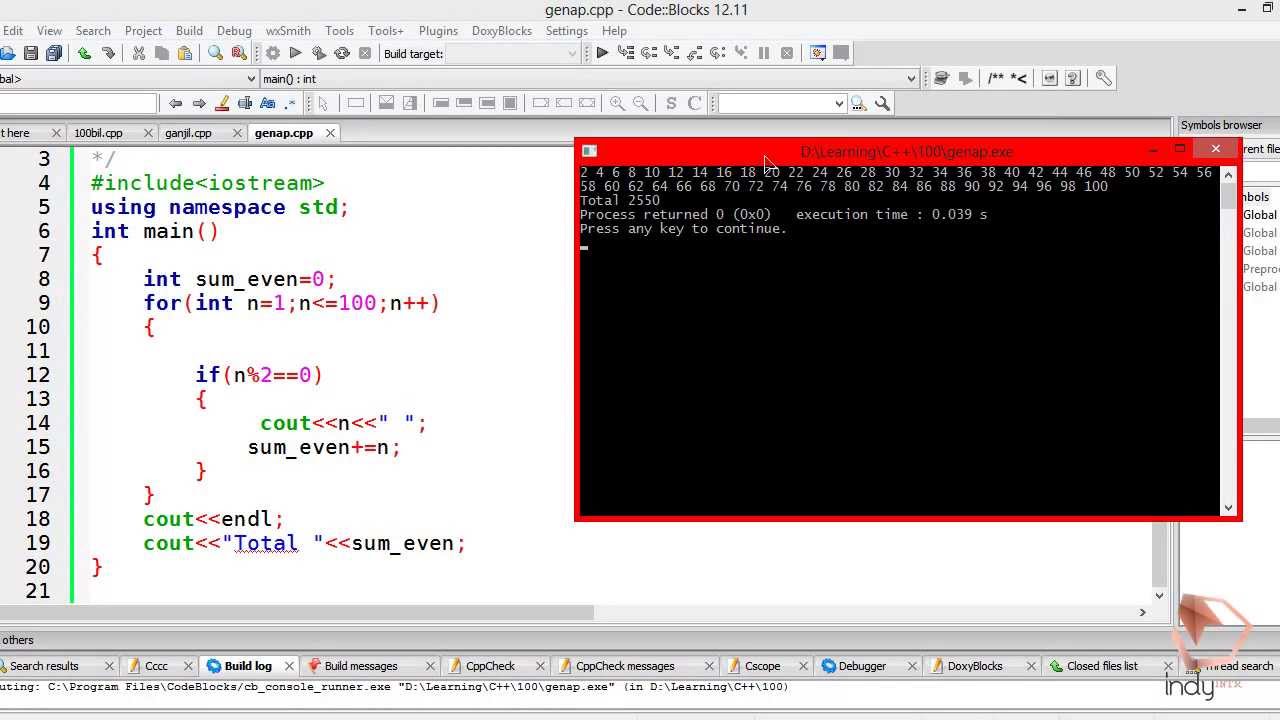
C Example Sum Of Even Integers Between 1 100 Youtube
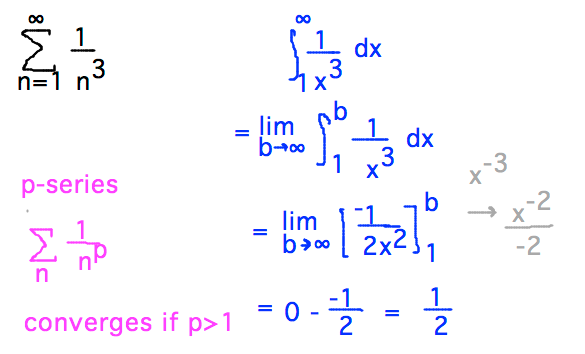
Geneseo Math 222 01 Integral Test

The Two Sequence Of Number 1 4 16 64 And 3 12 48 192 Are Mixed As Follows 1 3 4 12 16 48 64 192 One Of The Numbers In The Mixed In The Mixed Series Is Then Number Immediately Preceding Is

How To Add A Sequence Of Consecutive Odd Numbers 14 Steps

Sum Of N N Or N Brilliant Math Science Wiki
Web Maths Unsw Edu Au Mikeh Webpapers Paper25 Pdf
Q Tbn 3aand9gcs38bham4lp8on3ce2yk7nzepsxnqj6uxoxtwn4vvl5c2pbyhsv Usqp Cau



